1 引言
　　在輕工、化工等很多行業(yè)的過程控制中，被控對象大都帶有滯后特性，熱量、物料和信號等的轉(zhuǎn)移或轉(zhuǎn)換需經(jīng)過一定的時(shí)間，這便造成了許多過程存在大的滯后時(shí)間。無論控制作用如何，在滯后時(shí)間階段，控制作用對過程變量的影響是不可測的。更為重要的是，時(shí)間滯后導(dǎo)致了過程變量輸出不能迅速地響應(yīng)控制信號，這等于在這段時(shí)間內(nèi)反饋?zhàn)饔檬В答伿亲詣涌刂扑仨毜玫降男畔ⅰ?br>　　PID 控制方法是目前應(yīng)用最廣泛的控制策略之一，但若用PID 來控制具有顯著時(shí)間滯后的過程，則控制器輸出在滯后時(shí)間內(nèi)由于得不到合適的反饋信號保持增長，從而導(dǎo)致系統(tǒng)響應(yīng)超調(diào)大甚至使系統(tǒng)失控。通常PID 控制為了維持自動狀態(tài)必須明顯調(diào)低PID 參數(shù)，這就必然造成控制性能的降低。一般而言，PID 控制器能控制τ-T 比（滯后時(shí)間/時(shí)間常數(shù)）小于1 的過程，對于大τ-T 比的系統(tǒng)，則必須調(diào)低PID 參數(shù)，所以難免控制遲緩，品質(zhì)變差。史密斯預(yù)估器是處理具有大滯后過程的一種非常有用的控制方法，然而構(gòu)造史密斯預(yù)估器通常需要精確的過程模型，否則，其性能不能令人滿意。
　　2 從PID 到非線性PID
　　眾所周知，PID 控制算法因其結(jié)構(gòu)簡單、魯棒性好、可靠性高，在實(shí)踐中容易被理解和實(shí)現(xiàn)，可以以此為基礎(chǔ)發(fā)展許多高級控制策略，所以仍然廣泛應(yīng)用于工業(yè)過程控制中。
　　PID 調(diào)節(jié)器是一種理想的過程調(diào)節(jié)器，根據(jù)現(xiàn)代控制理論的觀點(diǎn)，PID 具有本質(zhì)的魯棒性、優(yōu)化控制特征和智能化。其控制原理是：利用負(fù)反饋獲得系統(tǒng)輸出與期望目標(biāo)的誤差信號e，作為PID 控制器的輸入，誤差信號的比例、積分、微分的線性組合，作為PID 控制器的輸出，即控制量u，用公式表示為：

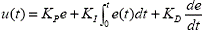
　　其中KP 是比例增益，KI 是積分增益，KD 是微分增益。
　　可見，PID 控制器輸出的控制量u 只是誤差信號的比例、積分、微分三部分分別乘以各自的增益參數(shù)以后的簡單相加，而各增益參數(shù)都是通過適當(dāng)整定方法得出的常數(shù)，由此便體現(xiàn)出了PID 控制律控制的局限性。因?yàn)榭刂葡到y(tǒng)的性能指標(biāo)通常要根據(jù)工業(yè)生產(chǎn)過程對控制的要求來制定，這種要求可概括為穩(wěn)定性、準(zhǔn)確性和快速性，所以PID 控制在實(shí)際應(yīng)用中的局限性就是：其輸出是誤差信號的比例、積分、微分的線性組合，但線性組合并非最佳選擇，理論分析和大量實(shí)踐表明，"線性組合"常引起快速性和超調(diào)量之間的矛盾，即不能同時(shí)滿足既快速達(dá)到理想值同時(shí)又盡量減小超調(diào)量這兩個(gè)性能要求。另外，這種簡單的結(jié)構(gòu)也決定其不可能對環(huán)境或控制對象模型參數(shù)的變化具有自適應(yīng)能力。
　　可見傳統(tǒng)線性PID 控制器在控制品質(zhì)上的局限性，主要來自以下幾個(gè)方面：
　　(1) 算法結(jié)構(gòu)的簡單性決定了PID 控制比較適用于SISO 最小相位系統(tǒng)，在處理大滯后、開環(huán)不穩(wěn)定過程等難控對象時(shí)，難以取得較好的控制效果，保證較好的動態(tài)性能。
　　(2) 結(jié)構(gòu)的簡單性同時(shí)決定了PID 控制只能確定閉環(huán)系統(tǒng)的少數(shù)主要零極點(diǎn)，閉環(huán)特性從根本上是基于動態(tài)特性的低階近似假定的。
　　(3) 出于同樣原因，決定了常規(guī)PID 控制器無法同時(shí)滿足快速跟蹤設(shè)定值和抑制擾動的不同性能要求。
　　由于以上原因，單純的線性PID 控制并不是大滯后系統(tǒng)的最佳控制策略，而且誤差的比例、積分、微分三部分的線性組合始終無法克服快速性和超調(diào)量之間的矛盾，故本文在此基礎(chǔ)上，采用了一種新型的PID 控制方法--非線性PID，以期既能兼顧傳統(tǒng)PID 的優(yōu)點(diǎn)又能改善其在對大滯后對象進(jìn)行控制時(shí)的控制效果。
　　3 非線性PID 控制器
　　要得到非線性PID，顧名思義就是找到合適的非線性函數(shù)對輸出控制量的計(jì)算公式 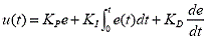 進(jìn)行改進(jìn)，使控制器的控制量輸出不再是控制誤差比例、積分、微分三部分的單純的線性相加，從而有望克服傳統(tǒng)PID 的局限性。具體的方法可以是通過非線性函數(shù)對e、 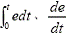分別進(jìn)行轉(zhuǎn)化，也可以利用非線性函數(shù)對它們的增益參數(shù)KP、KI、KD 進(jìn)行非線性轉(zhuǎn)換。
　　本文采用的非線性PID 的基本原理為：根據(jù)系統(tǒng)階躍響應(yīng)曲線，分段分析PID 控制器增益參數(shù)KP、KI、KD 應(yīng)有的變化趨勢，分別得出它們能夠滿足系統(tǒng)動態(tài)性能要求的曲線形狀，并由此選擇合適的非線性函數(shù)，本文采用了雙曲正割函數(shù)sech()和指數(shù)函數(shù)exp()來擬合這一曲線，使KP、KI、KD成為隨e(t)變化的變量，且其變化趨勢符合人們想達(dá)到的更高性能指標(biāo)的要求。
　　具體實(shí)現(xiàn)方法如下。
　　圖1 是一般的系統(tǒng)階躍響應(yīng)曲線，根據(jù)該曲線可以分析非線性PID 控制器增益參數(shù)的構(gòu)造思想。

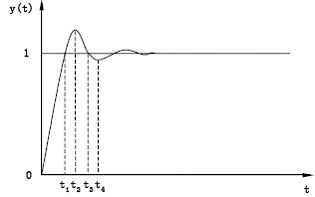
　　圖1 一般系統(tǒng)階躍響應(yīng)曲線

　　設(shè)計(jì)原理如下：
　　(1) 比例增益參數(shù)KP
　　在響應(yīng)時(shí)間0≤t≤t1 段，為保證系統(tǒng)有較快的響應(yīng)速度，比例增益參數(shù)KP 在初始時(shí)應(yīng)較大，同時(shí)為了減小超調(diào)量，希望誤差e 逐漸減小時(shí)，比例增益也隨之減??；在t1≤t≤t2 段，為了增大反向控制作用，減小超調(diào)，希望KP 逐漸增大；在t2≤t≤t3 段，為了使系統(tǒng)盡快回到穩(wěn)定點(diǎn)，并不再產(chǎn)生大的慣性，期望KP 逐漸減??；在t3≤t≤t4 段，期望KP 逐漸增大，作用與t1≤t≤t2 段相同。顯然，按上述變化規(guī)律，隨誤差e變化的大致形狀如圖2(a)所示，根據(jù)該圖可以構(gòu)造如下非線性函數(shù)：

　　式中，ap，bp，cp 為正實(shí)常熟。當(dāng)誤差e→∞時(shí)，KP 取最大值為ap＋bp ；當(dāng)e＝0 時(shí)，KP 取最小值為ap;bp為KP 的變化區(qū)間，調(diào)整cp 的大小可調(diào)整KP 變化的速率。
　　(2) 微分增益參數(shù)KD
　　在響應(yīng)時(shí)間0≤t≤t1 段，微分增益參數(shù)KD 應(yīng)由小逐漸變大，這樣可以保證在不影響響應(yīng)速度的前提下，抑制超調(diào)的產(chǎn)生；在t1≤t≤t2 段，繼續(xù)增大KD，從而增大反向控制作用，減小超調(diào)量。在t2 時(shí)刻，減小微分增益參數(shù)KD，并在隨后的t2≤t≤t4 段再次逐漸增大KD，抑制超調(diào)的產(chǎn)生。根據(jù)KD 的變化要求，在構(gòu)造KD 的非線性函數(shù)時(shí)應(yīng)考慮到誤差變化速率ev 的符號。KD 的變化形狀如圖2(b)所示，所構(gòu)造的非線性函數(shù)為：
　　Kd(e(t),ev(t))= ad + bd /(1+ (cd exp(ddsign(ev(t)).e(t)))
　　式中， ev = e 為誤差變化速率， ad，bd，cd，dd 為正實(shí)常熟，ad 為KD 的最小值，ad + bd為KD 的最大值，當(dāng)e＝0時(shí)，KD= ad + bd /(1 +cd) ，調(diào)整dd 的大小可調(diào)整KD 的變化速率。
　　(3) 積分增益參數(shù)KI
　　當(dāng)誤差信號較大時(shí)，希望積分增益不要太大，以防止響應(yīng)產(chǎn)生振蕩，有利于減小超調(diào)量；而當(dāng)誤差較小時(shí)，希望積分增益增大，以消除系統(tǒng)的靜態(tài)誤差。根據(jù)積分增益的希望變化特性，積分增益參數(shù)KI 的變化形狀如圖2(c)所示，其非線性函數(shù)可表示為：
　　KI (e(t))= aisech(cie(t))
　　式中，KI 的取值范圍為（0，ai），當(dāng)e＝0 時(shí)，KI 取最大值。ci 的取值決定了KI 的變化快慢程度。
　　則非線性PID 調(diào)節(jié)器的控制輸入為：

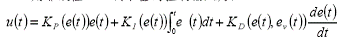
　　由上述分析可知，如果非線性函數(shù)中的各項(xiàng)參數(shù)選擇適當(dāng)，就能使控制系統(tǒng)既響應(yīng)快，又無超調(diào)現(xiàn)象。另外，由于非線性PID 調(diào)節(jié)器中的增益參數(shù)能隨控制誤差變化，因而其抗干擾能力,克服由大滯后對象的滯后特性帶來的影響能力也比常規(guī)線性PID 強(qiáng)，比常規(guī)線性PID 更加智能，有更強(qiáng)的自適應(yīng)能力和魯棒性，即便工況發(fā)生一定變化仍能保持較好的控制品質(zhì)，更適用于諸如大滯后系統(tǒng)等工況更加復(fù)雜的控制場合。

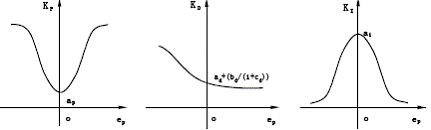
　　(a) KP 變化曲線   (b) KD 變化曲線    (c) KI 變化曲線
　　圖2 非線性增益調(diào)節(jié)參數(shù)變化曲線

　　4 溫度控制實(shí)驗(yàn)結(jié)果及分析
　　根據(jù)前面的研究和分析，考慮將該非線性控制方法用于對溫度這一工業(yè)控制中常見的具有大滯后特性的物理量進(jìn)行控制。溫度是工業(yè)控制的主要對象之一，其控制對象很多，且不盡相同。但工業(yè)中的溫度對象一個(gè)較為普遍的特點(diǎn)就是它們大都含有純滯后環(huán)節(jié)，容易引起系統(tǒng)超調(diào)和持續(xù)的振蕩。除此之外，溫度控制對象的參數(shù)一般會發(fā)生幅度較大的變化，從而導(dǎo)致溫度對象數(shù)學(xué)模型的不斷變化。這種隨機(jī)產(chǎn)生和不可準(zhǔn)確預(yù)計(jì)的變化，無疑地增加了溫度控制的難度。
　　因此，對于這種工況不斷發(fā)生變化且具有大滯后特性的控制場合，采用前面描述的非線性PID 控制器，以其優(yōu)于常規(guī)線性PID 控制器的自適應(yīng)能力和更完善的控制性能定能取得更好的控制效果。
　　本文采用貝加萊2003 PCC 作為控制器，通過B&R Automation Studio 操作系統(tǒng)進(jìn)行編程，利用非線性控制算法對陶瓷加熱片進(jìn)行加熱實(shí)驗(yàn)（系統(tǒng)結(jié)構(gòu)如圖3 所示）。通過溫度傳感器采集陶瓷片的實(shí)際溫度送入PCC 的溫度模擬量輸入模塊，并與溫度設(shè)定值進(jìn)行比較得出偏差，代入非線性PID控制算法算得控制量，再通過輸出量計(jì)算程序?qū)⒃摽刂屏哭D(zhuǎn)化為數(shù)字量控制加熱器的加熱頻率，即一個(gè)控制周期內(nèi)加熱時(shí)間的占空比，同時(shí)可在Automation Studio 環(huán)境下對控制過程進(jìn)行監(jiān)控，繪制trace 曲線圖。

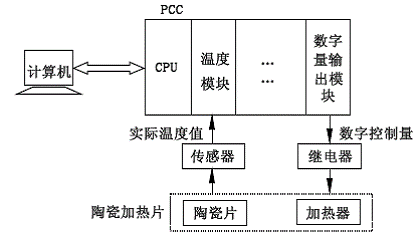
　　圖3 陶瓷片加熱溫控實(shí)驗(yàn)系統(tǒng)結(jié)構(gòu)圖
　　以下是實(shí)驗(yàn)過程中實(shí)際溫度變化響應(yīng)的trace 曲線圖。

 
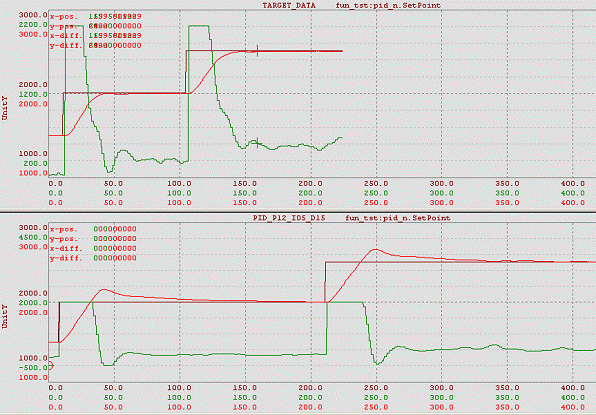
　　圖4 溫度跟蹤曲線示意圖
　　上圖：非線性PID 下圖：常規(guī)PID

　　由圖4 可以看出，非線性PID 控制器取得了明顯優(yōu)于線性PID 的控制效果。主要表現(xiàn)在三方面：
　　(1) 有效地抑制了超調(diào)，超調(diào)量很小，而線性PID 超調(diào)較為明顯；
　　(2) 大幅度縮短了調(diào)節(jié)時(shí)間，快速達(dá)到穩(wěn)態(tài)，而線性PID的穩(wěn)定時(shí)間大約是非線性PID 的四倍；
　　(3) 穩(wěn)態(tài)誤差小，穩(wěn)態(tài)性能好。
　　可見，在對例如溫度控制此類大滯后控制對象進(jìn)行控制時(shí)，采用適當(dāng)?shù)姆蔷€性函數(shù)對常規(guī)的線性PID 進(jìn)行改進(jìn)，既可以改善系統(tǒng)的自適應(yīng)能力，又能克服傳統(tǒng)線性PID 所固有的快速性和超調(diào)量難以兼顧的矛盾，完全可以在各個(gè)方面達(dá)到更好的控制性能要求，取得更優(yōu)良的控制品質(zhì)。
　　另外關(guān)于這一方法還存在兩個(gè)問題：
　　(1) 關(guān)于參數(shù)的整定。由上面的函數(shù)表述可以看出使用此控制器需要調(diào)節(jié)的參數(shù)較多，包括
　　ap、bp、cp、ad、bd、 cd、dd 、ai 、ci 共九個(gè)取代了原來的KP、KI、KD三個(gè)參數(shù)，對于這些參數(shù)的整定本文主要是根據(jù)實(shí)驗(yàn)情況和經(jīng)驗(yàn)進(jìn)行調(diào)節(jié)，一旦獲得合適的參數(shù)就能得到較為優(yōu)良的控制效果且抗擾動性和自適應(yīng)性很強(qiáng)一般情況下不需要重新整定。也可以通過一些辦法進(jìn)行簡化，例如使aP＝0，bP 取負(fù)數(shù)，則KP 和KI 的非線性函數(shù)合二為一，可將參數(shù)由9 個(gè)簡化到5～6 個(gè)，方便現(xiàn)場調(diào)試人員的參數(shù)調(diào)整。
　?。?）關(guān)于所采用的非線性函數(shù)。本文根據(jù)對控制性能要求的分析采用了sech()函數(shù)和exp()函數(shù)，取得了良好的控制效果，但也可根據(jù)實(shí)際情況將其它的更簡單實(shí)用的非線性特性引入PID 算法得到非線性PID 控制器，同理也可以找到相應(yīng)的非線性函數(shù)對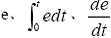 進(jìn)行轉(zhuǎn)化?？傊?，通過更進(jìn)一步的研究完全可以找到更好的非線性特性設(shè)計(jì)出效率更高的非線性PID 控制器。
　　5 結(jié)論
　　本文針對大滯后控制對象，在分析傳統(tǒng)線性PID 控制的原理和優(yōu)缺點(diǎn)的基礎(chǔ)上，本著繼承其優(yōu)點(diǎn)克服其缺點(diǎn)的原則，介紹并采用了一種非線性PID 控制器對溫度這一大滯后控制對象進(jìn)行控制，并取得了理想的實(shí)驗(yàn)結(jié)果。實(shí)驗(yàn)結(jié)果表明，用此種方法對溫度進(jìn)行控制響應(yīng)快、超調(diào)小、穩(wěn)態(tài)誤差小，控制品質(zhì)明顯優(yōu)于傳統(tǒng)線性PID。但在參數(shù)調(diào)整和非線性函數(shù)的選取等方面還有很大探討空間，今后可在這些方面做進(jìn)一步研究，使非線性PID 控制方法進(jìn)一步發(fā)展和完善，能夠廣泛應(yīng)用于工業(yè)控制過程。
　　參考文獻(xiàn)：
　　[1] 劉立志. 微型計(jì)算機(jī)控制技術(shù)[M]. 濟(jì)南: 山東大學(xué)出版社, 1996。
　　[2] 劉金琨. 先進(jìn)PID 控制及其MATLAB 仿真[M]. 北京:電子工業(yè)出版社, 2003。
　　[3] 周重陽, 王寧. 大純滯后工業(yè)對象的神經(jīng)元控制器[J]. 自動化儀表,2002, 23(2): 9～12
　　[4] 韓瑞珍. PID 控制器參數(shù)模糊自整定研究[D]. 浙江工業(yè)大學(xué)碩士論文, 2001, 12。
　　[5] 盧振芳. 智能溫度控制系統(tǒng)的設(shè)計(jì)[D]. 南京航空航天大學(xué)碩士論文,2001, 2。
　　作者簡介：張凌云（1979），女，山東萊蕪人，碩士，研究方向?yàn)榭刂评碚摰膽?yīng)用。